Problem Statement
Jenny is chasing Toby over an infinite plane, in order to stab him in the face. Out of love. Toby can set up 3 wards, and place himself anywhere. Jenny is instantly vaporised if she steps within the radius of any of Toby's wards, while Toby is immune from the wards. Can Jenny kill Toby?
This is an ICPC contest problem. My solution is implemented as an illustration. Jenny is a triangle and Toby is a square. Jenny and Toby are green whenever it is possible for Jenny to kill Toby, and red whenever she cannot.
The canvas is of a fixed size, but you can imagine it stretches to infinity. The canvas's border does not actually provide any protection for poor Toby.
Controls
Use interactive mode or button mode. Unfortunately, interactive mode does not work on mobile. Sorry :( In button mode, press buttons to randomly generate wards, as well as the position of Toby and Jenny. In interactive mode, First three clicks are the wards. Mouse down to set center, draw mouse to set radius. Next click is Toby. All subsequent clicks place Jenny.
Design
This is a cool ICPC problem dealing with simple geometry
There are a few edge cases, but the overall idea is simple: both Jenny and Toby must be outside the wards, and they must be on the same side of the triangle formed by the centers of the wards, if the triangle is "closed". Testing whether a point is inside a circle can be done in the following way:
(x - x_0)^2 + (y - y_0)^2 ≤ r ^ 2To check whether the wards form a closed "triangle", the distance between each two ward centers must be no more than the sum of their radii.
dist(c_i, c_j) ≤ r_i + r_jFor every pair of wards i and j.
Testing whether a point is contained in a triangle is a bit more tricky. My basic idea is that for any compact 2D shape (like a triangle), if you imagine walking along the outside of it, a point inside the shape will always be on the same side of you. In the example below, the point is always to the left.
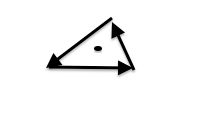
For a polygon, this means that between any two points adjacent points on the polygon A and B (where B comes after A in the 'walking' sequence) and a point inside the polygon, p, the angle formed by AB and Ap is always of the same sign (when that angle is between π and -π). This is equivalent to saying that the cross product between those two vectors always points in the same direction, or the z-coordinate of the cross-product has always has the same sign. The z-coordinate of the cross-product can be computed with this code:
(u_x·v_y - u_y·v_x)And now the rest is relatively simple.
The edge-cases are a bit gross, because you have to think about what happens when Toby is on the edge of the triangle/circle, versus when Jenny is on the edge. However, if you add enough if statements, anything is possible!

